[コンプリート！] odds versus probability 151788-Odds versus probability

 Probability vs Odds vs Log Odds All these concepts essentially represent the same measure but in different ways In the case of logistic regression, log odds is used We will see the reason why log odds is preferred in logistic regression algorithm Probability of 0,5 means that there is an equal chance for the email to be spam or not spamFrom a mathematics standpoint, let's assume p = number of possible positive outcomes of an event q = number of possible negative outcomes of an event Therefore p q = total number of outcomes of an event The probability of a positive event occurr Statistics — Probability vs Odds 📅 Probability and odds are two basic statistic terms to describe the likeliness that an event will occur They are often used interchangeably in causal conversation or even in published material However, they are not mathematically equivalent because they are looking at likeliness in

Betting Guide Odds Versus Probability Odds Margin Calculator

Odds versus probability

Odds versus probability- As you can see, the idea of probability is relatively simple But the idea of odds, on the other hand, is a bit more complicatedmostly because there's more than one way to write them The most common way is what's called "bookmakers odds"Mean Logodds vs Mean probability 300;

Odds Ppt Download

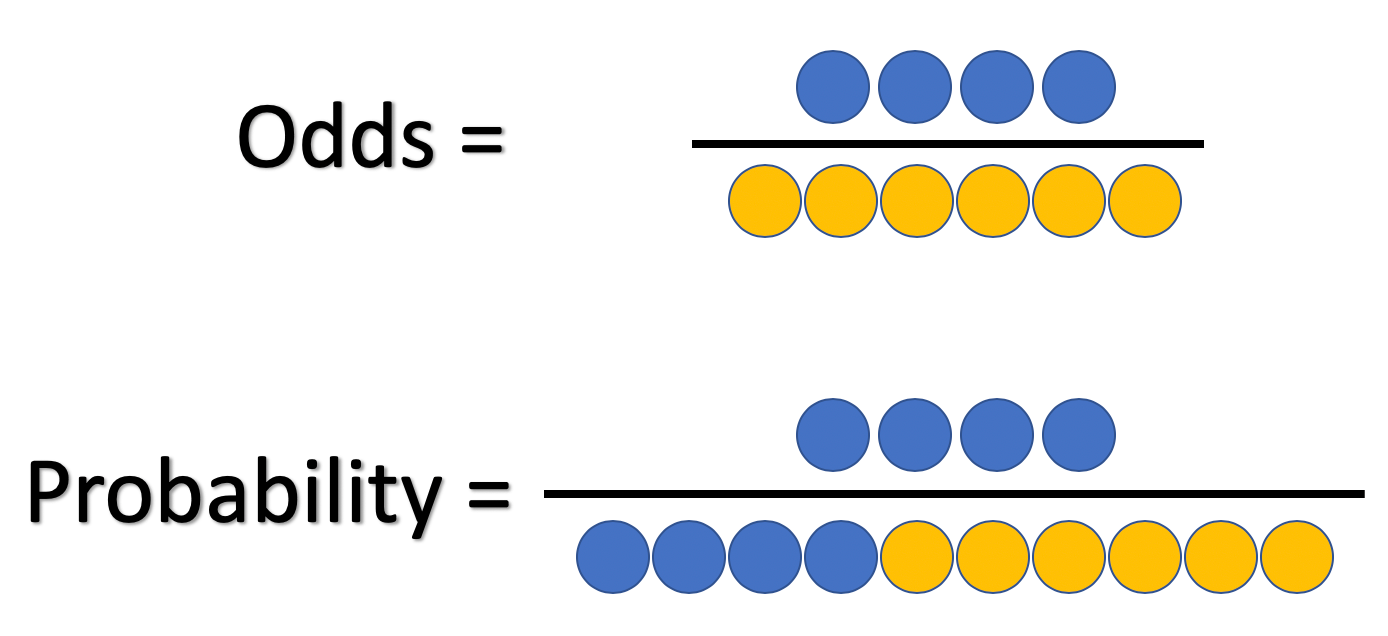
 Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 against Odds ratio vs probability ratio Ask Question Asked 1 year, 6 months ago Active 5 months ago Viewed 553 times 8 5 $\begingroup$ An odds is the ratio of the probability of an event to its complement $$\text{odds}(X) = \frac{P(X)}{1P(X)}$$ An odds ratio (OR) is Probability theory is an interesting area of statistics concerned with the odds or chances of an event happening in a trial, eg getting a six when a dice is thrown or drawing an ace of hearts from a pack of cards To work out odds, we also need to have an understanding of permutations and combinations

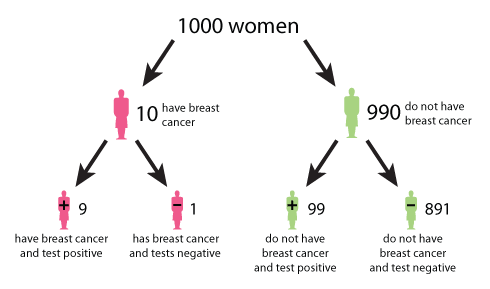
Categories Metaculus Itself Make a Prediction Prediction Note this question resolved before its original close time All of your predictions came after the resolution, so you did not gain (orOdds are based on the probability that an event will ever occur 2 Probability only measures the chances that an event will occur against the total number of times the even will occur;Posttest odds = Pretest odds * Likelihood ratio In equation above, positive posttest probability is calculated using the likelihood ratio positive, and the negative posttest probability is calculated using the likelihood ratio negative Posttest probability = Posttest odds / (Posttest odds

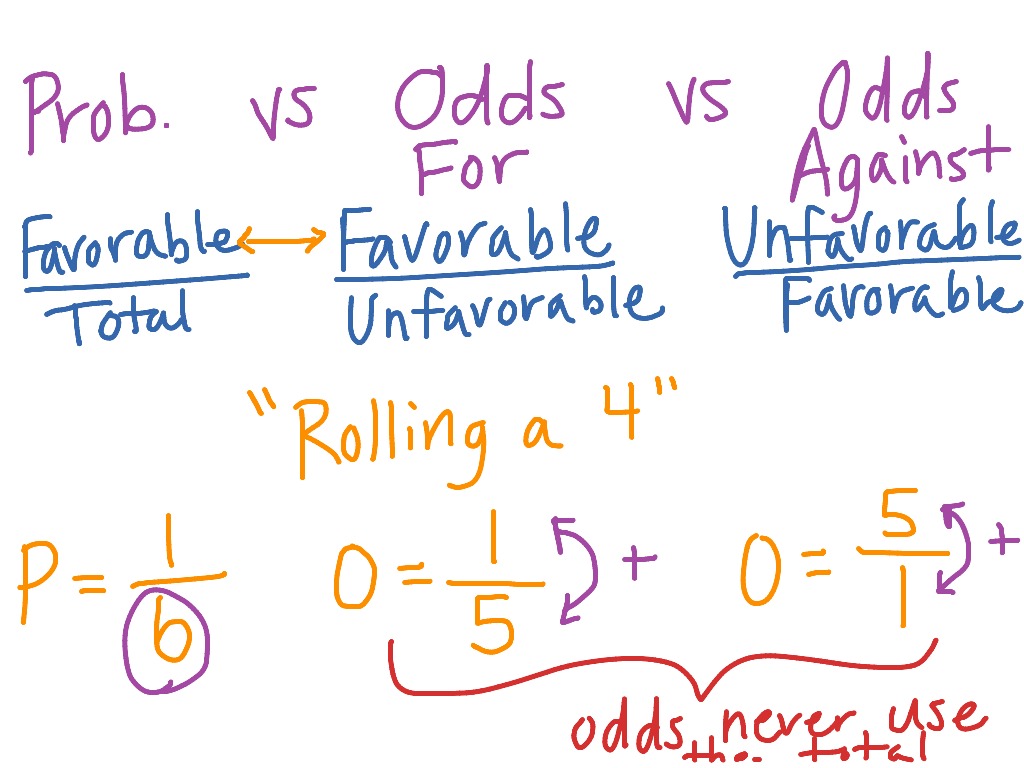
 Equal odds are 1 1 success for every 1 failure 11 Equal probabilities are 5 1 success for every 2 trials Odds can range from 0 to infinity Odds greater than 1 indicates success is more likely than failure Odds less than 1 indicates failure is more likely than success Probability can range from 0 to 1 Odds Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 So the odds is 025/075 or 13 (or 033 or 1/3 pronounced 1 to 3 odds) Moving back and forth Probability in Terms of Odds for and against the Event Odds for and against an event represent a ratio of the desired outcomes versus the field In other words, the odds for an event are the ratio of the number of ways the event can occur to the number of ways the event does not occur Thus

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

1

Of probability, chances and odds are not the same For instance, the odds in favor of A are P(A) / P(Ac) = (3/4)/(1/4) = 3/1 It is said that the odds in favor of A are 31 or that A is an event twice as likely as "not A" Therefore, the odds of A occurring are expressed in the scale of the probability of "A not occurring" Odds versus Probability Odds is less intuitive than probability (probably wouldn't say "my odds of dying are 1/4") No less legitimate mathematically, just not so easily understood Also important because the log odds of the outcome is given by the coefficient of a predictor in a logistic regressionThe odds of not rolling a 5 or 6 is the inverse 42 This is because there are 4 events that produce the specified outcome of "not rolling a 5 or 6" (rolling a 1,2,3, or 4) and two that do not (rolling a 5 or 6) The probability of an event is different, but related, and can be

Simple Probability Definition Probability The Chance Some Event

Understanding Uncertainty Visualising Probabilities Plus Maths Org

Conversely, if odds are very small (1/1000), probability will also be very small, close to 0 Probability/Odds Conversion Converting probabilities into odds, we simply divide the probability by 1 less the probability, eg, if the probability is 25% (025), the odds are 025/075, which can also be expressed as 1 to 3 or 1/3 or 0333 Odds Converting Odds to Probability Simply add the 2 components of the odds together to make a new denominator, and use the old numerator eg If the odds are 35, or 3 to 5, the probability is 3 ÷ (35) = 3/8 = 375% Converting Probability to Odds Take the probability, and divide it by its compliment = (1itself) egMany people wrongfully assume odds and probabilities are the same thingThey're definitely not, as there's a significant difference between saying there are

Odds Versus Probability Math Showme

Demystifying The P Value

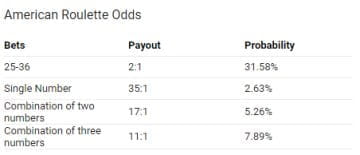
 The odds are 1626 and probability is 016% If you're playing poker long enough you will somewhat regularly encounter the aces vs kings scenario at a table A formula to estimate the probability for this to happen at a 9 player table is This formula slightly underestimates the actual probability which is a little bit higher Odds can be helpful when we want to compare how much larger one probability is relative to another An event with a probability 75% has odds of 75 to 25 We can simplify this to 3 to 1 This means that the event is three times more likely to occur than not occur Cite this Article The Ask Dr Math forum has several entries on odds versus probability Summarizing, one way to conceptualize (nontechnically) the probability of an event is the number of ways that an event can occur divided by the total number of possible outcomes The probability of heads in a fair coin flip is 1/2 (50 percent)

Betting Guide Odds Versus Probability Odds Margin Calculator

Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium

Odds is a see also of probability As nouns the difference between odds and probability is that odds is the ratio of the probabilities of an event happening to that of it not happening while probability is the state of being probable;Money Line Implied Probability The following chart shows how likely a team is to win based off the odds This is helpful in handicapping because you can see just what percentage of your wagers you need to win at each given money line in order to profit The left chart is to be used for favorites, the right for underdogs Odds, chances and probability are just different ways of expressing the likelihood of an event In your example of the jackpot that hits on average once per 100,000 spins, the probability of hitting the jackpot is Many people have difficulty relating to a decimal number So another, equivalent way to express the likelihood of hitting

Estimating An Odds Ratio From A Gwas Only Reporting The P Value Sean Harrison Blog

What Are The Odds The Annals Of Thoracic Surgery

Odds The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than probabilityIn poker, pot odds are the ratio of the current size of the pot to the cost of a contemplated call Pot odds are often compared to the probability of winning a hand with a future card in order to estimate the call's expected value Converting odds ratios to and from percentages Odds are most commonly expressed as ratios, but converting them to Odds ratios work the same An odds ratio of 108 will give you an 8% increase in the odds at any value of X Likewise, the difference in the probability (or the odds) depends on the value of X So if you do decide to report the increase in probability at different values of X, you'll have to do it at low, medium, and high values of X

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

Math 30 2 Probability Odds Acceptable Standards 50 79 The Student Can Express Odds For Or Odds Against As A Probability Determine The Probability Ppt Download

 Calculating Implied Probability with American Odds Implied probability refers to the likelihood of a particular outcome suggested by the odds Figuring it out involves converting odds into a percentage, which indicates the likelihood that event will happen vs the alternativeRISK AND ODDS DEFINITIONS "Risk" refers to the probability of occurrence of an event or outcome Statistically, risk = chance of the outcome of interest/all possible outcomes The term "odds" is often used instead of risk "Odds" refers to the probability of occurrence of an event/probability of the event not occurringMean Logodds vs Mean probability 1000;

Bayesian Analysis A Brief Introduction Robert West University

Free Guide The Winning Lottery Formula Based On Combinatorics And Probability Theory Lotterycodex

Odds measure the chances for and the chances against an event ever occurring 3 Probability ensures that an event will occur;Mean Logodds vs Mean probability 100; Odds vs Probability While odds and probability are related mathematical concepts, the two are also distinctly different The probability of something occurring represents the fraction of times you'd see it happen over several trials If you have a 50% probability of catching the bus, that number represents the idea that you will catch the bus half the time

The Math Behind Betting Odds Gambling

Betting Odds Explained How Are Football Odds Calculated

 The differences between odds and probability are discussed in the points given below The term 'odds' is used to describe that if there are any chances of the occurrence of an event or not As against, While odds are expressed in the ratio, the probability is either written in percentage form orMean vs Median LogOdds 1000; The probability that an event will occur is the fraction of times you expect to see that event in many trials Probabilities always range between 0 and 1 The odds are defined as the probability that the event will occur divided by the probability that the event will not occur A probability of 0 is the same as odds of 0

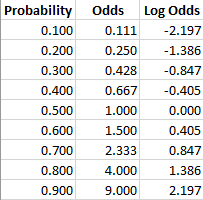
Log Odds Definition And Worked Statistics Problems

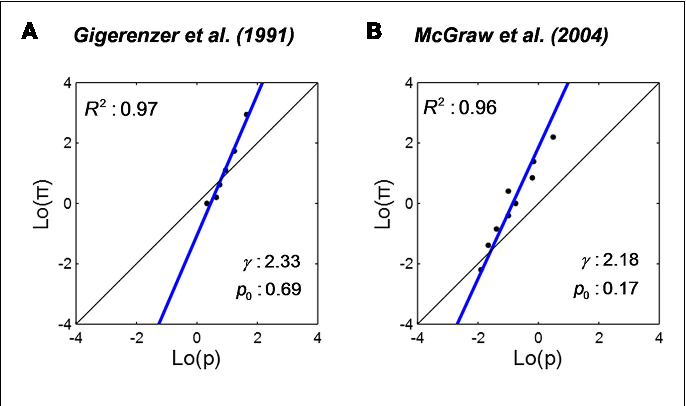
Figure 5 From Ubiquitous Log Odds A Common Representation Of Probability And Frequency Distortion In Perception Action And Cognition Semantic Scholar

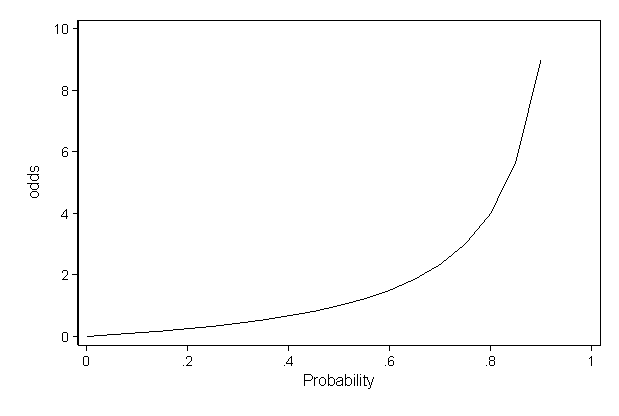
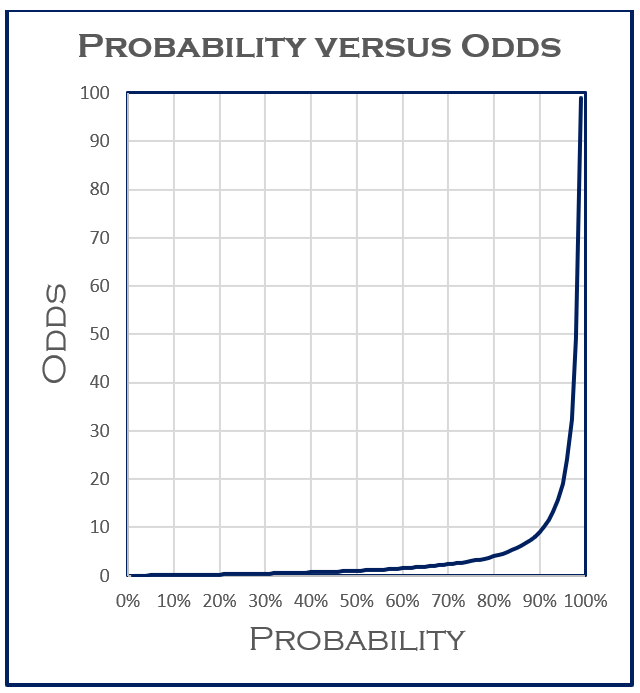
Odds are ratios of a player's chances of losing to his or her chances of winning, or the average frequency of a loss to the average frequency of a win If a player owns 1 of 4 tickets, his/her probability is 1 in 4 but his/her odds are 3 to 1 That means that there are 3 chances of losing and only 1 chance of winning Summary 1 Probability is a mathematical measure of how often an event will occur;Labs(title ="probability versus odds") 000 025 050 075 100 0 50 100 150 odds p probability versus odds Finally, this is the plot that I think you'llfind most

True Odds Calculator Find Probabilities Fair Odds Margin

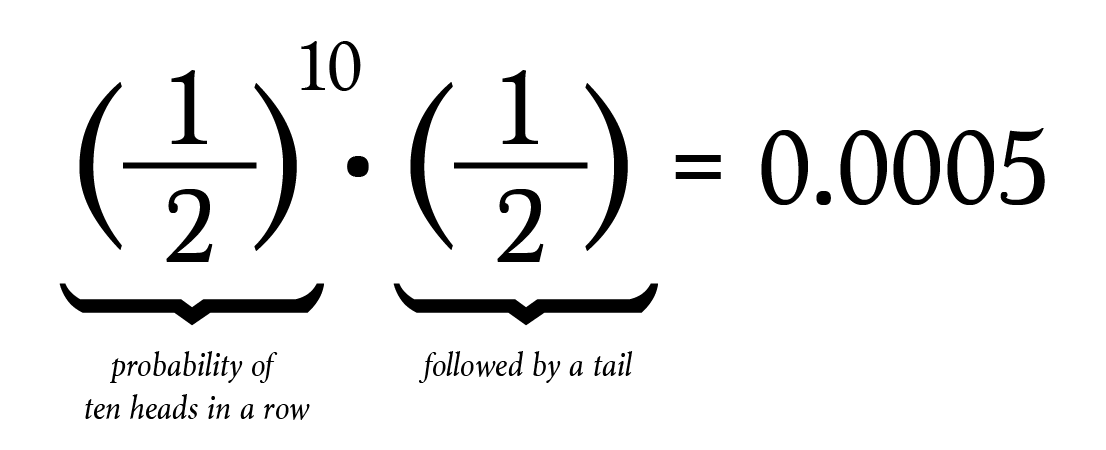
That Common Misconception About Probability By Brett Berry Math Hacks Medium

Probability and Order Versus Evolution BY HENRY M MORRIS, PHD SUNDAY, JULY 01, 1979 One of the strongest direct evidences for special creation is the existence of innumerable highly complex systems in the universe, systems composed of components occurring in a pattern of "order" rather than disorderHow to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, and Probability versus Odds A case study While the definitions of these terms can overcomplicate matters, the best way to describe them in action is to look at the coin toss challenge It provides the perfect setting for an explanation of the difference between these two statistical terms because there will only ever be one of two outcomes heads

Odds Vs Probability Vs Chance Data Science Central

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

Odds, are given as (chances for success) (chances against success) or vice versa If odds are stated as an A to B chance of winning then the probability of winning is given as P W = A / (A B) while the probability of losing is given as P L = B / (A B)Using an example of decimal odds, a candidate has 2 odds to win the next election If so, the implied probability is 4545%, or ( 1 2 2 × 1 0 0) \begin {aligned} &\left ( \frac { 1 } { 22BioEpi540W 6 Applications of Probability in Epidemiology Page 11 of 17 b Odds("comparison of two complementary (opposite) outcomes") In words, the odds of an event "E" is the chances of the event occurring in comparison to

Chapter 6 Choosing Effect Measures And Computing Estimates Of Effect Cochrane Training

Probability And Odds Youtube

A probability, on the other hand, is a measure or estimation of how likely is it that an event will come to pass, or that a statement is true Probabilities are given a value between 0 or 1, where 0 is a 0% chance of the event happening, ie it will not happened, and

Probability Odds Odds Ratio Youtube

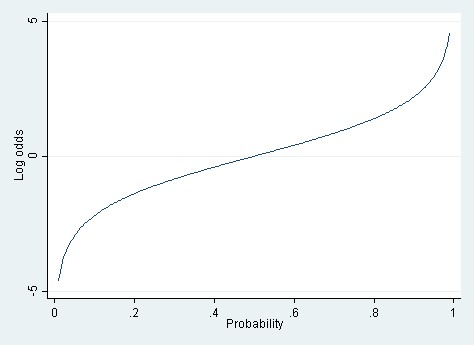
Linear Vs Logistic Probability Models Which Is Better And When Statistical Horizons

Converting Between Probability And Odds Mathwoes Youtube

Probability Vs Odds In Favour Or Against An Event Examples Youtube

Odds Probability And The Lottery Lotterycodex

Odds Probability The Difference Explained With Examples

Odds Ratio Sage Research Methods

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

Binary Logistic Regression With Odds Ratios Calculated For The Download Table

Binary Logistic Regression With Odds Ratios Calculated For The Download Table

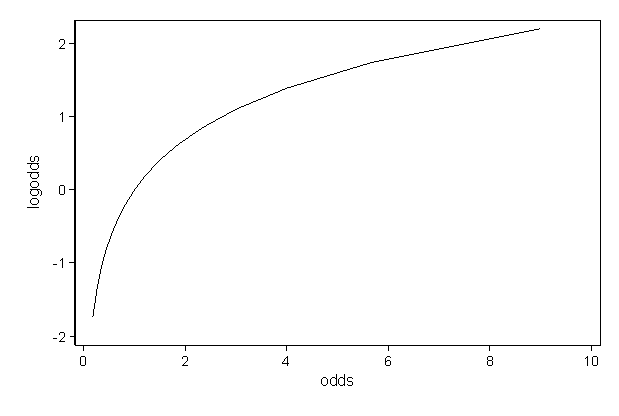
What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

Odds And Probability

How To Read And Calculate Sports Odds Everything You Need To Know Betting 101

Odds Ppt Download

What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

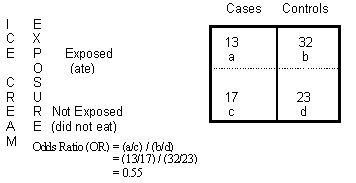
Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1

Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1

Bayes Rule Odds Form Intro Math 1 Arbital

The Difference Between Relative Risk And Odds Ratios The Analysis Factor

1

A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence

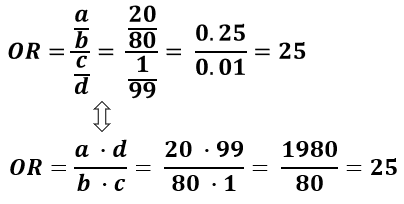
Odds Ratio Calculator Calculate Odds Ratio Confidence Intervals P Values For Odds Ratios

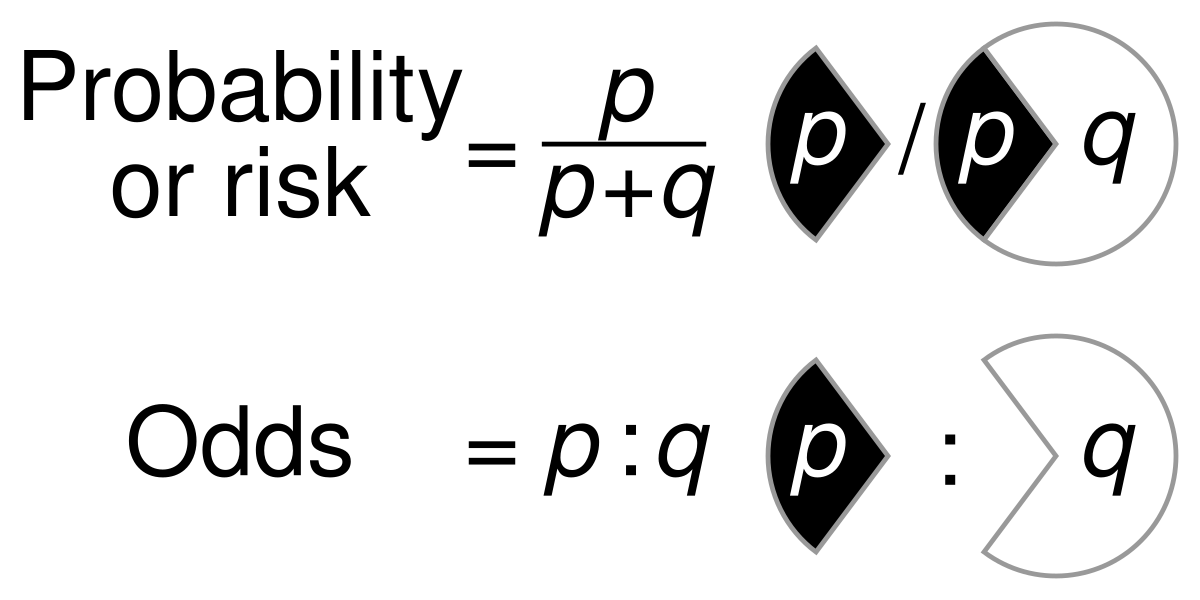
File Probability Vs Odds Svg Wikimedia Commons

Estimates Of Odds Ratios Of Daily Probability Of Diarrhea In The Download Scientific Diagram

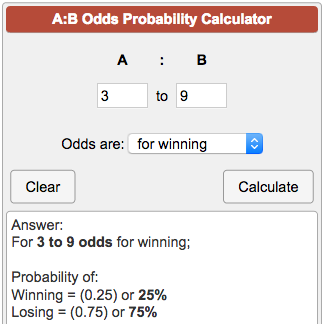
Odds Probability Calculator

Classification Methods And Assessment

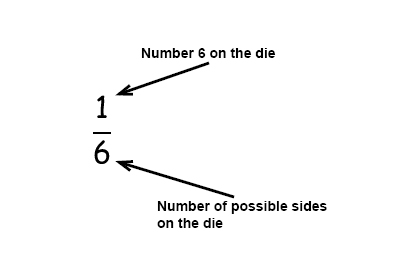
Probability Of Events Pre Algebra Probability And Statistic Mathplanet

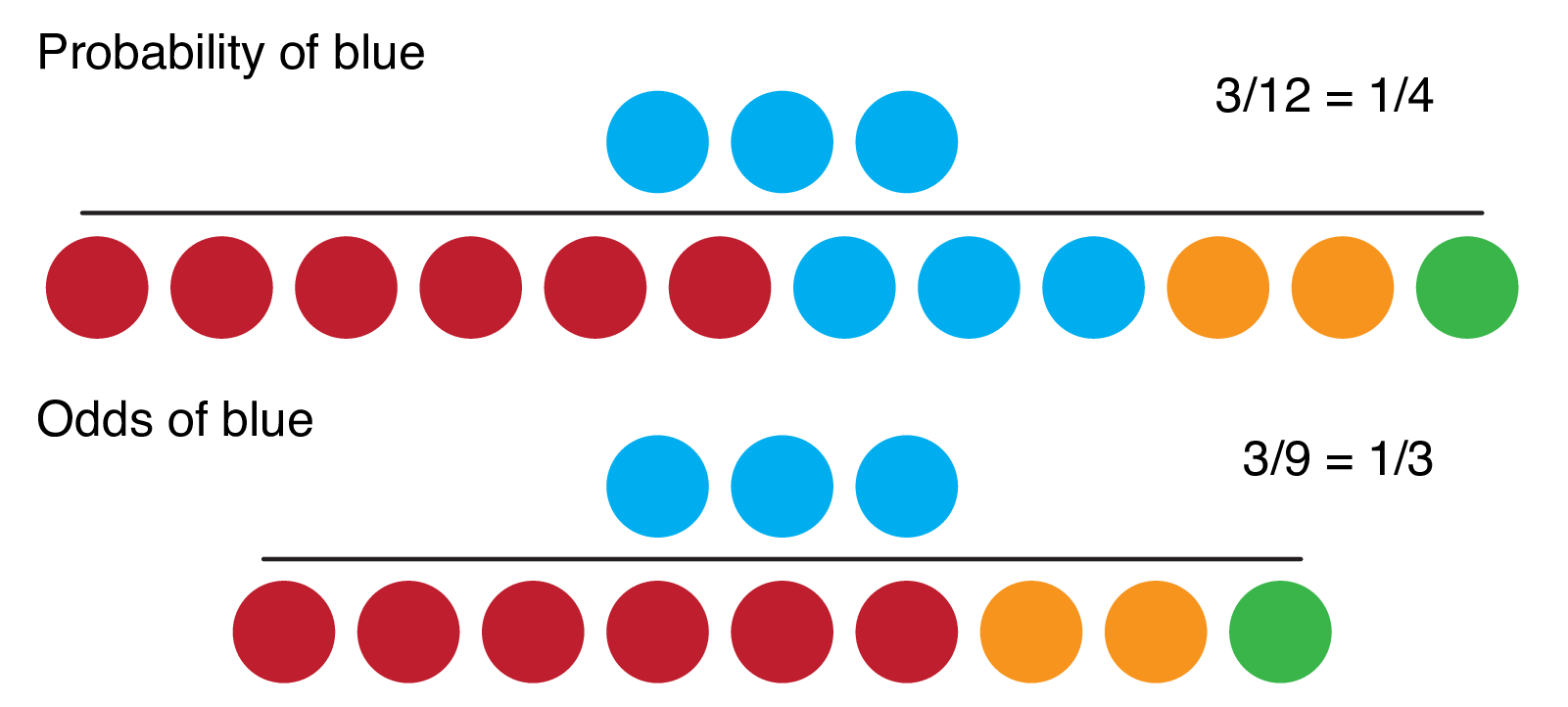
9 2 Binary Logistic Regression R For Health Data Science

Faq How Do I Interpret Odds Ratios In Logistic Regression

Odds Likelihood Ratios Guide To Diagnostic Tests

The Bounded Rationality Of Probability Distortion Pnas

Odds

Statistics Of Dice Throw

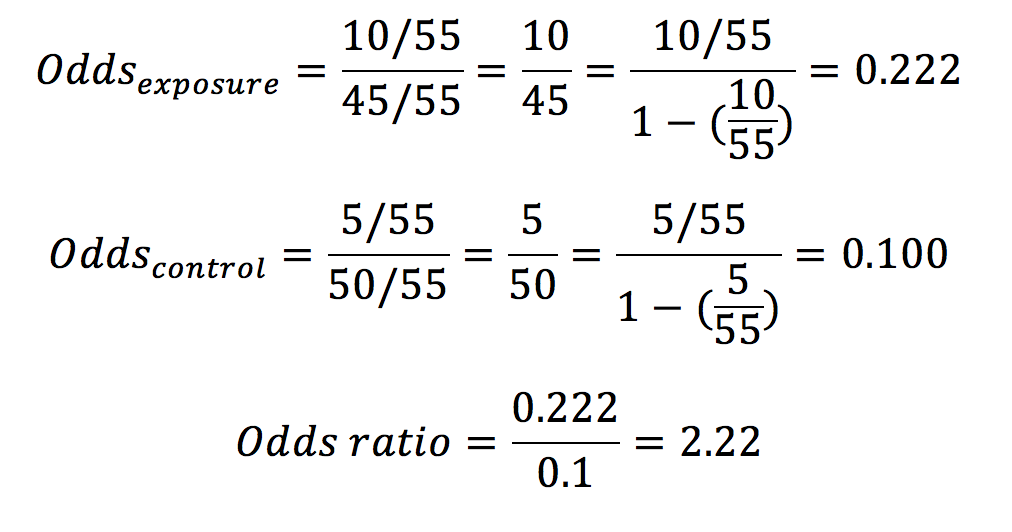
Statistics For Medical Students Geeky Medics

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

Odds Ratios Versus Relative Risk

Www Jstor Org Stable

Odds Ratio Wikipedia

Ctspedia Ctspedia Oddsterm

Logistic Regression

May The Odds Be In Your Favour Financially

Faq How Do I Interpret Odds Ratios In Logistic Regression

Odds Ratio Calculation And Interpretation Statistics How To

Ctspedia Ctspedia Oddsterm

Odds

Log Odds Ratio Analytics Function Series By Analyttica Datalab Medium

Ppt Basic Probability Powerpoint Presentation Free Download Id

Implied Probability Betting Math Made Simple 21 Update

How To Read And Calculate Sports Odds Everything You Need To Know Betting 101

Probability Vs Odds Youtube

E Birbeck 7 04 Simple Probability Definition Probability The Chance Some Event Will Happen It Is The Ratio Of The Number Of Ways Ppt Download

How To Calculate Odds 11 Steps With Pictures Wikihow

The Difference Between Probability And Odds

Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1

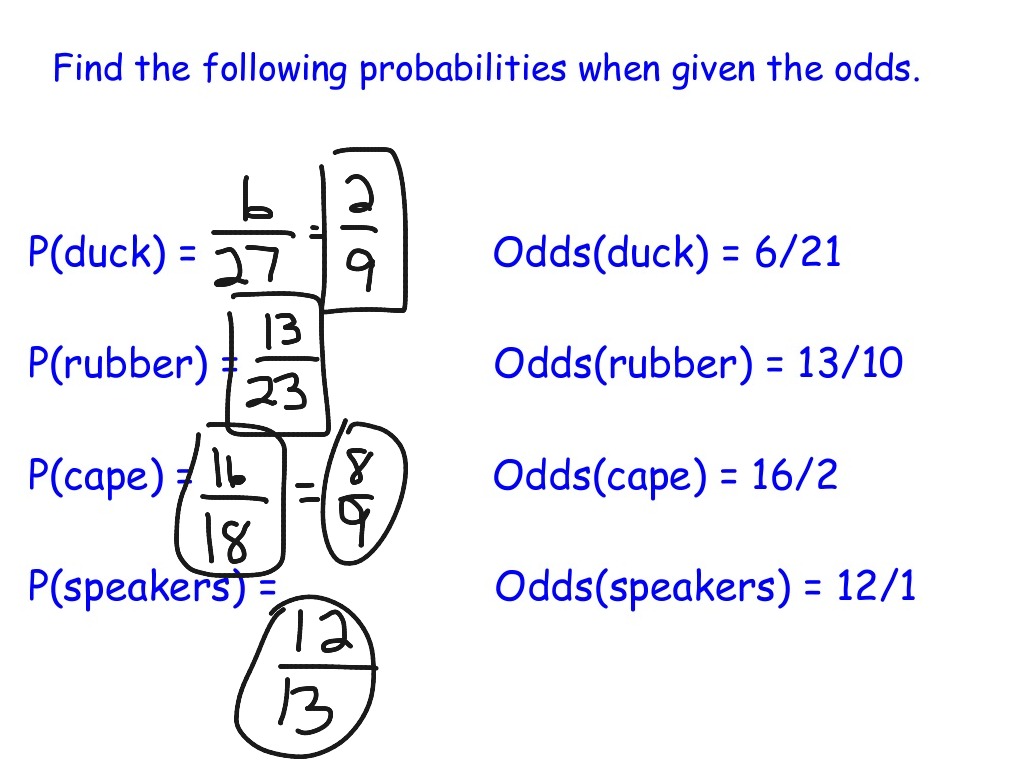
Probability Probability Vs Odds Lesson Math Statistics Showme

What Is Predicted Probability Magoosh Statistics Blog

What Is An Odds Ratio And How Do I Interpret It Critical Appraisal

Estimates Of Odds Ratios Of Daily Probability Of Diarrhea In The Download Scientific Diagram

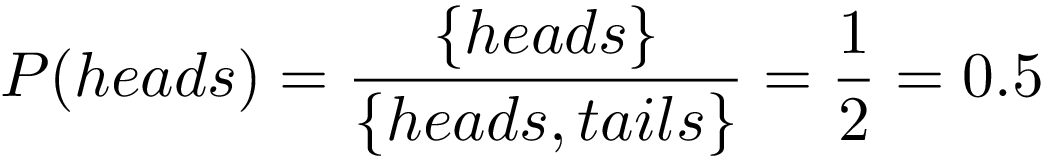
Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

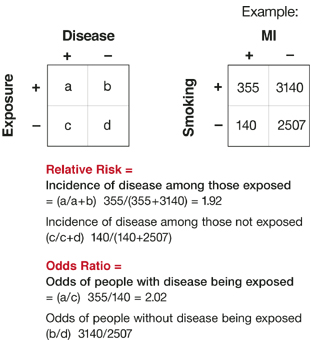
Relative Risks And Odds Ratios What S The Difference Mdedge Family Medicine

Odds Ratios And Risk Ratios Youtube

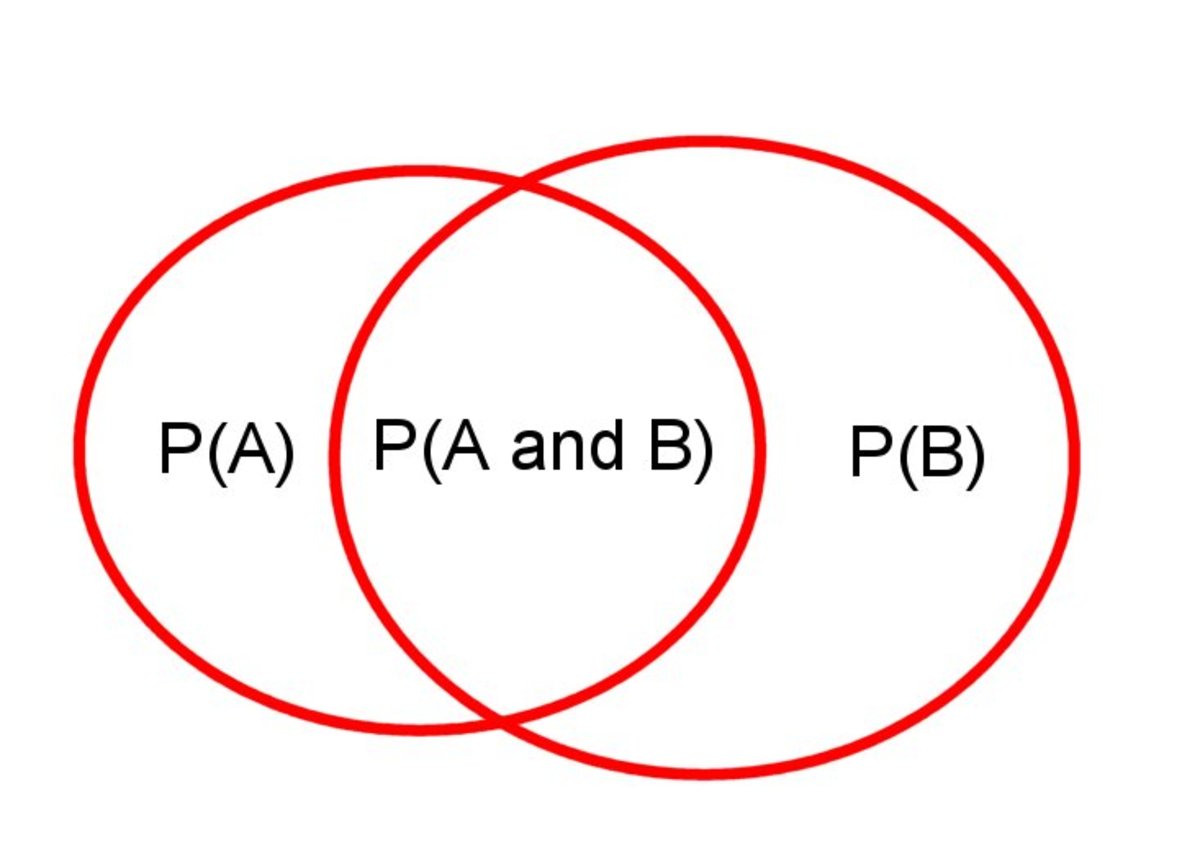
Probability Of A And B A Or B Statistics How To

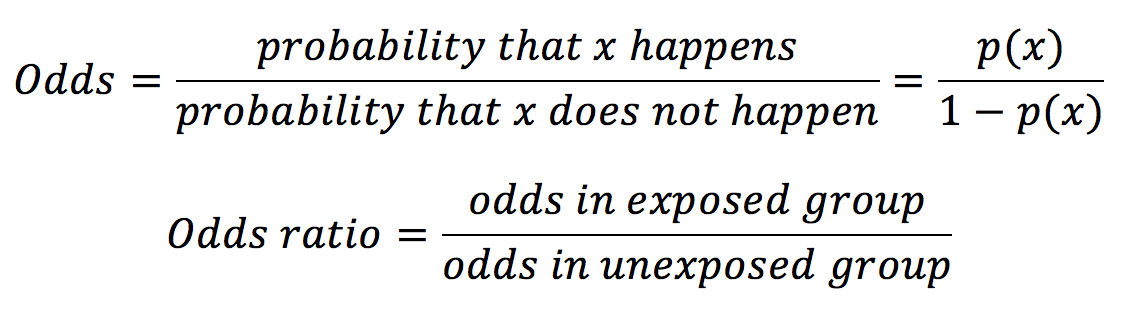
Statistics For Medical Students Geeky Medics

Odds Introduction Arbital

Odds And Probability

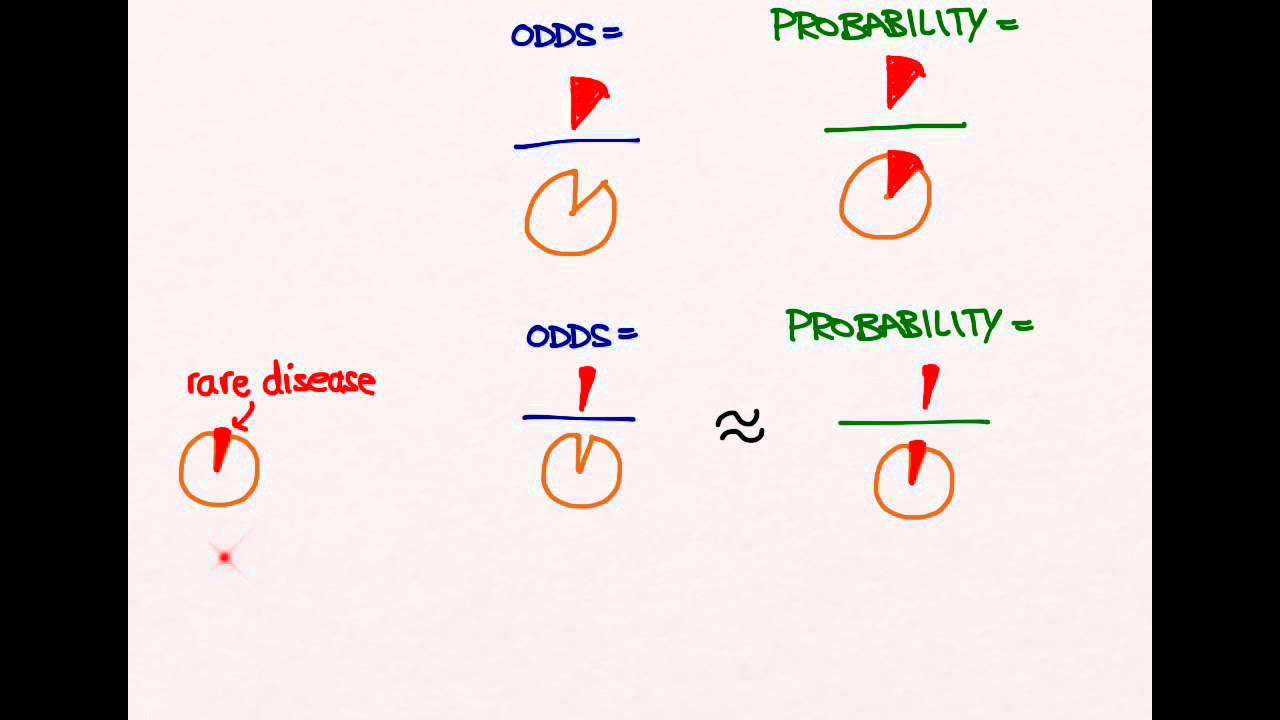
What Are The Odds Stats With Cats Blog

Odds Likelihood Ratios Guide To Diagnostic Tests

Confidence Intervals And P Values

How To Find The Probability Of An Event And Calculate Odds Permutations And Combinations Owlcation

How Sports Betting Odds Work How To Read Odds Explanation Video

How To Calculate Odds 11 Steps With Pictures Wikihow

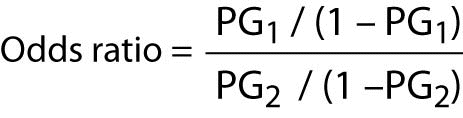
The Odds Ratio Calculation Usage And Interpretation Biochemia Medica

Statistics 12 Probability Vs Odds Stats Seandolinar Com

Comparing Probability Odds For And Odds Against Youtube

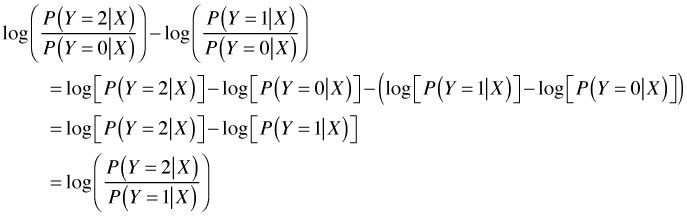
Lecture 38 Monday April 16 12

What Are The Odds Stats With Cats Blog

Probability Vs Odds In Favour Or Against An Event Examples Youtube

Logistic Regression

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

How To Calculate Odds 11 Steps With Pictures Wikihow

Incoming Term: odds versus probability,